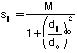.
We show how a basic pairwise alignment procedure
can be improved to more accurately align conserved structural
regions, by using variable, position-dependent gap penalties that
depend on secondary structure and by taking the consensus of a
number of suboptimal alignments. These improvements, which are
novel for structural alignment, are direct analogs of what is
possible with normal sequence alignment. They are feasible for
us since our basic structural alignment procedure, unlike others,
is so similar to normal sequence alignment. We further present
preliminary results that show how our procedure can be generalized
to produce a multiple alignment of a family of structures. Our
approach is based on finding a "median" structure from
doing all possible pairwise alignments and then aligning everything
to it.
Structural alignment involves finding equivalences between sequential positions in two proteins. As such, it is similar to sequence alignment. However, in structural alignment the equivalences are not found by comparing two strings of characters but rather by optimally superimposing two structures and finding the regions of closest overlap in three-dimensions (figure 1). Structural alignment is becoming increasingly important as the number of known protein structures increases exponentially. Currently, there are more than 5000 structures in the Protein Data Bank (exactly, 5208 as of September 1995). Structural alignment is also very important because it is usually thought of as providing a standard or target for sequence alignment. That is, one will be a long way towards achieving accurate sequence alignment if one can align two homologous but highly diverged proteins (say, with low percent identity of ~15 %) on the basis of sequence as well as on the basis of structure.
A number of procedures for automatic structural alignment and comparison have been developed (Taylor & Orengo, 1989; Russell & Barton, 1993; Holm & Sander, 1993; Sali & Blundell, 1990; Godzik & Skolnick, 1994; Artymiuk et al., 1989; Subbiah et al., 1993; Laurents et al., 1994). These procedures for structural alignment have detected many interesting similarities in protein structure - e.g. the globin-colicin similarity (Holm & Sander, 1993b) and have been used to cluster the whole structure databank on the basis of structural similarity (Holm & Sander, 1994).
There are often two goals in structural alignment. One is oriented toward sensitivity, finding remote similarities to a query structure in a large structural database. Another is more oriented towards accuracy, finding as good as possible an alignment between structures which one already knows are similar. To achieve the first goal one wants as fast as possible an alignment algorithm, whereas for the second goal speed is not a primary consideration. It is this second goal that will occupy us here.
The next step after pairwise structural alignment is obviously multiple structural alignment, simultaneously aligning three or more structures together. There are currently a number of approaches for doing this (Taylor et al., 1994; Sali & Blundell, 1990; Russell & Barton, 1993). These methods can proceed by analogy to multiple sequence alignment (Taylor, 1987, 1988, 1990), building up an alignment one structure at a time.
Multiple structural alignment is valuable for a number of reasons.
It is an essential first step in the construction of consensus
structural templates, which aim to encapsulate the information
in a family of structures (Johnson et al., 1993; Altman &
Gerstein, 1994, Gerstein & Altman, 1995). It can also form
the nucleus for a large multiple sequence alignment of a family
(Bashford et al., 1987; Sander & Schneider, 1991; Pascarella
& Argos, 1992; Gerstein et al., 1994; Kapp et al., 1995).
That is, highly homologous sequences can be aligned to each structure
in the multiple alignment.
Here we present two modifications our previously described alignment
procedure (Subbiah et al., 1993; Laurents et al., 1994) to make
it more accurate and better able to align conserved core regions:
variable gap penalties and noisy, suboptimal alignment. These
modifications, which are novel to structural alignment, are direct
analogs of common techniques in sequence alignment - for instance,
for a discussion of variable gap penalties see Lesk et al. (1986),
Smith & Smith (1992), and Vingron & Waterman (1994), and
for a discussion of suboptimal alignment, see Zuker (1991) and
Waterman et al. (1992). They are feasible for our structural alignment
procedure because it is so similar to normal sequence alignment,
involving repetitive application of Needleman-Wunsch (1971) dynamic
programming. In contrast, many of the other commonly used approaches
to structural alignment, which involve comparing distance matrices
for two structures (Taylor & Orengo, 1989; Holm & Sander,
1993) or looking for similarities in a graph (Artymiuk et al.,
1989), would not be modifiable in this way. After describing how
our alignment procedure can be made more accurate, we sketch how
it can be extended in straightforward fashion to generate multiple
structural alignments, based on aligning all structures to a central
or median structure. Our results in the area of multiple structural
alignment are only preliminary and will be described in detail
elsewhere (Gerstein & Levitt, submitted).
The procedure we use for pairwise structural alignment, described in Subbiah et al. (1993) and Laurents et al. (1994), is based on iterative application of dynamic programming. As such it is a simple generalization of Needleman-Wunsch sequence alignment (Needleman & Wunsch, 1971). As shown in figure 2, one starts with two structures in an arbitrary orientation. Then one computes all pairwise distances between each atom in the first structure and every atom in the second structure. This results in a inter-protein distance matrix where each entry dij corresponds to the distance between atom i in the first structure and atom j in the second one. This distance matrix can be converted into a similarity matrix sij, similar to the one used in sequence alignment, by application of the following formula:
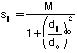.Here M is the maximum score of a match, which is arbitrarily chosen to be 20. do is the distance at which the similarity falls to about half its maximum value (i.e. dij =do Æ sij =0.45M). do is taken here to be 5 Å - reflecting the intrinsic length-scale of protein structural similarity. This is a little more than 3 times the length of a C-C bond (1.52 Å) and is larger by a about third than the usual distance between Ca atoms (3.8 Å).
One applies dynamic programming to the similarity matrix to generate a "sum matrix" and get equivalences. If this were normal sequence alignment, one would be finished at this point since dynamic programming gives the optimal equivalences. However, this is not the case for structural alignment. So one takes these equivalences and uses them to fit the first structure onto the second one. Then one repeats the procedure, finding all pairwise distances and doing dynamic programming to get equivalences. One repeats this over and over until it converges on the same set of equivalences. In practice, the iteration is tried from a number of different starting points, and the one that gives the best match, measured in terms of RMS deviation after doing a fit, is taken. One gets different starting points (or initial orientations) from doing fits based on different sets of initial equivalences (e.g. random, based on simple sequence matching, etc.).
We have tried a number of approaches toward improving the accuracy of the simple pairwise structural alignment algorithm presented above.
Using Cb atoms
The simplest improvement was to use Cb rather than Ca atoms for the computation of distances dij. Using Cb atoms makes misalignments by one residue in helices and especially strands more difficult. Misalignments by a single residue are not serious in terms of matching the overall fold but give nonsensical alignments in detail. For instance, in the case of strands they often lead to mismatching of hydrophobic and hydrophilic residues.
Secondary Structure Dependent Gap Penalties
Because of the similarity between our structural alignment procedure and normal sequence alignment, it is possible to incorporate variable, position-dependent gap penalties into the alignment in a very straightforward fashion. Since we know the secondary structure of the two proteins we are aligning (e.g. from DSSP, Kabsch & Sander, 1983) we can make it more difficult to introduce a gap at a position in a secondary structure (i.e. strand or helix). This is similar to sequence alignment methods that make the penalty for opening a gap depend on where it starts (Lesk et al., 1986; Smith & Smith, 1992; Vingron & Waterman, 1994).
We derived specific values for the gap penalties by empirically
testing them on a number of protein families. We found that as
the gap opening penalty is decreased in secondary structure relative
to that in loops and coils, one obviously increases the number
of spurious gaps in strands and helices. This suggests that very
high gap penalties in strands and helices might work well. However,
we also found that such high gap penalties make it more difficult
to align secondary structural elements (which often vary slightly
in size); in fact, a penalty that is too high leads to completely
mismatching secondary structures. (For instance, instead of aligning
two helices of slightly different size through introducing a gap
into the longer helix, the program might introduce many gaps into
a loop preceding one helix and align this helix against a loop
and the second against the introduced gaps). The specific values
we chose are a compromise between these two competing effects.
We always set the gap extension penalty to be a small constant
value (0.025 M). We arranged the gap opening penalties for each
structure into a vector a(k),
indexed by the sequence position i or j. Initially, the a(k)
values were set to 2 in sheets and helices and 1 otherwise. a(k)
is then smoothed (by convolution with a gaussian) and rescaled
so that the overall average gap penalty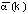 
is half the maximum match score M.
As described in figure 3, the introduction of variable gap penalties makes the dynamic programming rather complex, though it is still possible to achieve in roughly N2 operations (where N is the average size of the sequences being aligned).
Noisy, Suboptimal Structural Alignment
One of the goals in accurate structural alignment is to separate out those regions that match really well from those that match only partially well. We achieve this be doing a number of noisy structural alignments and taking the consensus. What is meant by a noisy alignment is described below in detail.
In normal dynamic programming, one builds up a sum matrix Sij from the similarity matrix sij, where each entry in Sij represents the best possible score one would get by starting at the beginning of the alignment and creating an alignment that ends by equivalencing position i in the first sequence with position j in the second sequence. As shown in figure 4, to find the overall optimum path, one usually imagines tracing back through this sum matrix starting from the entry with the maximum score. At each aligned point (i, j), one selects as the next aligned point the entry in the previous part of the matrix with the highest score - i.e. the point k,l such that Skl is maximum and k<i and l<j . Consequently, at each step in the traceback one is in a sense optimizing a score. If one deviates off this optimal path, one gets a suboptimal path or suboptimal alignment. One way to systematically deviate off this path is to do the traceback in a Monte-Carlo fashion, always choosing the next point if it is much higher than its neighbors, but sometimes choosing a non-optimal neighbor (in a Boltzmann fashion) if it has nearly the same score. If this is done one will get a variety of different suboptimal but still relatively high-scoring tracebacks through the matrix.
The same effect can be achieved in a somewhat simpler fashion by adding an element of random noise to both the match score sij (and the gap opening and extension penalty). Here we take the noise to be between ± 7.5 % of the maximum match score M.
To highlight the most accurately aligned regions of a structure, we can generate a number of these noisy sub-optimal alignments. Then we can take only the part of the alignment that is the same for each. This is shown for one particular case in figure 4, where the 434 repressor protein is aligned with myoglobin. The most similar helices are clearly conserved in the different suboptimal alignments.
We found it possible to form a multiple structural alignment from evaluating the results of all pairwise alignments (Gerstein & Levitt, submitted). We have tried to do this in a fairly straightforward fashion. After doing all pairwise alignments, we have picked the structure that is on average closest to all other structures. This is in the sense the "median" structure in the "cluster" of all the structures. We then align everything to this.
This presents one obvious problem: If position i in the median structure (i-in-median) aligns with position j in a second structure (j-in-2) and with position k in a third structure (k-in-3), we would align all three positions together. However, this is only really a true multiple alignment if k-in-3 aligns to j-in-2 in a pairwise fashion. Consequently, one possible internal check on the multiple alignment is to see whether at each position it is consistent with each automatically generated pairwise alignment.
Another (better) way check our multiple alignments is to compare them to manually produced multiple structural alignments. This simultaneously checks internal consistency and also whether the individual pairwise alignments are correct. In figure 5 we show sample multiple structural alignments of two protein families, the dihydrofolate reductases and the globins. These are checked against manual alignments (from Gerstein et al., 1994). We compare a manually generated multiple alignments against an automatically generated one by "aligning" them as best we can and then counting the number of mismatches. We only count mismatches in structurally conserved regions as certain regions of the protein structure, particularly some surface loops, are impossible to align correctly. As is evident our multiple alignment procedure is relatively successful in getting the alignment of both proteins correct.
We have described an approach toward generating an accurate multiple structural alignment of a family of protein structures. This approach is an extension of a previously described method for pairwise structural comparison. It incorporates secondary-structure dependent gap penalties and a core consensus alignment from a number of noisy alignments. We show that an accurate multiple structural alignment is achieved for two protein families, one all-a and another a/b, using the very straightforward approach of taking the median structure and aligning everything to it.
Availability of Results on the Internet
We make available over the Internet supplementary material relevant to this paper (e.g. manual and automatically generated alignments). Go to the following URL:
Acknowledgments
MG is supported by a Damon-Runyon Walter-Winchell fellowship (DRG-1272). ML acknowledges support from the Department of Energy (grant 2HDZ-477).
Altman, R. & Gerstein, M. 1994. Finding an Average Core Structure: Application to the Globins. Proceedings of the Second International Conference on Intelligent Systems in Molecular Biology. Menlo Park, CA: AAAI Press.
Artymiuk, P. J.; Mitchell, E. M.; Rice, D. W. & Willett, P. 1989. Searching Techniques for Databases of Protein Structures. J. Inform. Sci. 15: 287-298.
Bashford, D.; Chothia, C. & Lesk, A. M. 1987. Determinants of a Protein Fold: Unique Features of the Globin Amino Acid Sequences. J. Mol. Biol. 196: 199-216.
Bernstein, F. C.; Koetzle, T. F.; Williams, G. J. B.; Meyer, E. F., Jr; Brice, M. D.; Rodgers, J. R.; Kennard, O.; Shimanouchi, T. & Tasumi, M. 1977. The protein data bank: a computer-based archival file for macromolecular structures. J. Mol. Biol. 112: 535-542.
Gerstein, M. & Altman, R. 1995. Average core structures and variability measures for protein families: Application to the immunoglobulins. J. Mol. Biol. 251: 161-175.
Gerstein, M.; Sonnhammer, E. & Chothia, C. 1994. Volume Changes on Protein Evolution. J. Mol. Biol. 236: 1067-1078.
Godzik, A. & Skolnick, J. 1994. Flexible algorithm for direct multiple alignment of protein structures and sequences. CABIOS 10: 587-596.
Gribskov, M. & Devereux, J. 1992. Sequence Analysis Primer. New York: Oxford University Press.
Holm, L. & Sander, C. 1993. Protein Structure Comparison by Alignment of Distance Matrices. J. Mol. Biol. 233: 123-128.
Holm, L. & Sander, C. 1993. Structural alignment of globins, phycocyanins and colicin A. FEBS Lett. 315: 301-306.
Holm, L. & Sander, C. 1994. The FSSP database of structurally aligned protein fold families. Nuc. Acid Res. 22: 3600-3609.
Johnson, M. S.; Overington, J. P. & Blundell, T. L. 1993. Alignment and searching for common protein folds using a databank of structural templates. J. Mol. Biol. 231: 735-752.
Kabsch, W. & Sander, C. 1983. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-bonded and Geometrical Features. Biopolymers 22: 2577-2637.
Kapp, O. H.; Moens, L.; Vanfleteren, J.; Trotman, C. N. A.; Suzuki, T. & Vinogradov, S. N. 1995. Alignment of 700 globin sequences: Extent of amino acid substitution and its correlation with variation in volume. Prot. Sci. 4: 2179-2190.
Laurents, D. V.; Subbiah, S. & Levitt, M. 1994. Different Protein Sequences Can Give Rise to Highly Similar Folds Through Different Stabilizing Interactions. Prot. Sci. 3: 1938-1944.
Lesk, A. M.; Levitt, M. & Chothia, C. 1986. Alignment of amino acid sequences of distantly related proteins using variable gap penalties. Prot. Eng. 1: 77-78.
Needleman, S. B. & Wunsch, C. D. 1971. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 48: 443-453.
Orengo, C. A. 1994. Classification of protein folds. Curr. Opin. Struc. Biol. 4: 429-440.
Orengo, C. A.; Flores, T. P.; Taylor, W. R. & Thornton, J. M. 1993. Identifying and Classifying Protein Fold Families. Prot. Eng. 6: 485-500.
Pascarella, S. & Argos, P. 1992. A Databank Merging Related Protein Structures and Sequences. Prot. Eng. 5: 121-137.
Russel, R. B. & Barton, G. B. 1993. Multiple Protein Sequence Alignment from Tertiary Structure Comparisons. Assignment of Global and Residue Level Confidences. Proteins 14: 309-323.
Sali, A. & Blundell, T. L. 1990. The definition of general topological equivalence in protein structures: A procedure involving comparison of properties and relationships through simulated annealing and dynamic programming. J. Mol. Biol. 212: 403-428.
Sander, C. & Schneider, R. 1991. Database of Homology-Derived Protein Structures and the Structural Meaning of Sequence Alignment. Proteins: Struc. Func. Genet. 9: 56-68.
Smith, R. F. & Smith, T. F. 1992. Pattern induced multi-sequence alignment (PIMA) algorithm employing secondary structure dependent gap penalties for use in comparative protein modelling. Prot. Eng. 5: 35-41.
Subbiah, S.; Laurents, D. V. & Levitt, M. 1993. Structural similarity of DNA-binding domains of bacteriophage repressors and the globin core. Curr. Biol. 3: 141-148.
Taylor, W. R. 1987. Multiple sequence alignment by a pairwise algorithm. CABIOS 3: 81-87.
Taylor, W. R. 1988. A flexible method to align large numbers of biological sequences. J. Mol. Evol. 28: 456-474.
Taylor, W. R. 1990. Hierarchial method to align large numbers of biological sequences. Meth. Enz. 183: 456-473.
Taylor, W. R.; Flores, T. P. & Orengo, C. A. 1994. Multiple Protein Structure Alignment. Prot. Sci. 3: 2358-2365.
Taylor, W. R. & Orengo, C. A. 1989. Protein Structure Alignment. J. Mol. Biol. 208: 1-22.
Vingron, M. & Waterman, M. S. 1994. Sequence alignment and penalty choice. Review of concepts, case studies and implications. J. Mol. Biol. 235: 1-12.
Waterman, M. S.; Eggert, M. & Lander, E. 1992. Parametric sequence comparisons. Proc. Natl. Acad. Sci. USA 89: 6090-6093.
Zuker, M. 1991. Suboptimal sequence alignment in molecular biology:
alignment with error analysis. J. Mol. Biol. 221: 403-420.
Figure 1: Structural Alignment. This figure shows a sample structural alignment of two globins (1mbd and 1ecd, see figure 6). The aligned positions are indicated by small, gray CPK spheres.
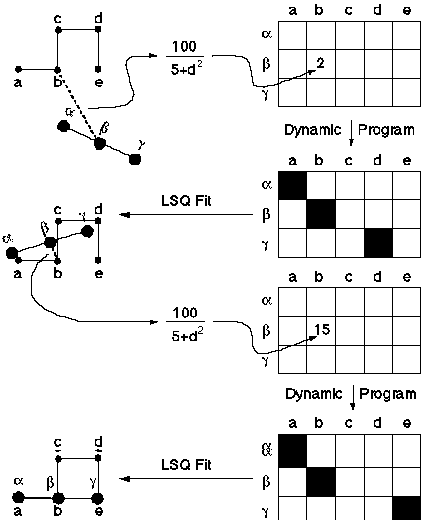
Figure 2: Schematic showing how pairwise structural alignment works. TOP-LEFT shows two structures (abcde and abg) in a random initial orientation. All pairwise distances are calculated between atoms in abcde to those in abg. These are converted into similarities (see text) and put into a matrix (TOP-RIGHT). Normal dynamic programming is performed on this matrix to find equivalences between atoms in the two structures (TOP-MID-RIGHT). Unlike sequence alignment, these equivalences are not globally optimal . To refine them, they are used to fit abg onto abcde in a least-squares sense. This gives the structures a new relative orientation as shown in MID-LEFT. Then the procedure is repeated: all pairwise inter-molecular distances are calculated between the structures (MID-LEFT), a matrix of similarities is formed (BOT-MID-RIGHT), and dynamic programming is done (BOT-RIGHT). This gives a second set of equivalences. These are used to refit the structures (BOT-LEFT), and everything is repeated iteratively until the procedure converges - i.e. there is no change in the equivalences between iterations.
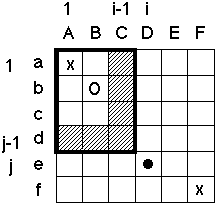
Figure 3: The Complexities Introduced by Variable Gap Penalties. In normal sequence alignment (Needleman & Wunsch, 1971), one constructs a sum matrix Sij (shown below) where each entry represents the best possible score for an alignment that ends with position i and j equivalenced. In building up this matrix, one often makes the assumption (e.g. see Gribskov and Devereux, 1992) that if i and j are aligned (" " in figure) the best previous alignment must have ended in either the previous row (i-1) or column (j-1) (hashed). This is equivalent to assuming that the following situation never occurs:
This is reasonable for sequence alignment. However, in structural alignment one often wants pieces in both structures to be unequivalenced, making it is necessary to allow for this sort of double mismatch. (This would happen, say, if one had two proteins with similar overall folds where the residues corresponding to a peripheral helix in one locally refolded into a strand in the other.) One allows for double mismatches by no longer assuming that if i and j are aligned the best previous alignment lies in the hashed region but rather allowing it to occur anywhere in the block 0 to i-1, 0 to j-1 (outlined box, where the best previous alignment is shown by an "o"). Especially with variable gap penalties, this makes the dynamic programming rather complex. If one does not use any tricks or make any assumptions, the alignment will be very slow (O(N4), where N is the length the sequences being compared). However, by assuming that the gap penalty always increases with increasing length of gap, one can use a caching scheme to make the overall performance N2. This assumption is satisfied if gap penalties in both i and j directions have the form of a(k) + (l-1)b(k), where a is a gap opening penalty, b is a gap extension penalty, l is the gap length, and k is a row or column index (i or j) depending on whether this is a deletion or insertion.
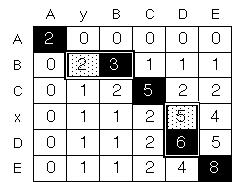
Figure 4: Suboptimal Paths. This figure illustrates the idea of possible suboptimal paths in tracing back through the sum matrix Sij (see figure 3). Here a sum matrix is shown for aligning ABCxDE with AyBCDE with a match score of 2 and gap-opening penalty of -1. To get the optimum traceback (which is indicated by black boxes), one starts at the overall maximum and progressively finds each succeeding maximum in the matrix (e.g. 8 Æ 6 Æ 5 Æ 3 Æ 2). However, if one perturbs the values in the matrix by the addition of random noise (e.g. by adding a series of random numbers Ri, between -2 and 2, to each matrix element), one may find slightly suboptimal alignments (indicated by gray boxes) now have favorable scores. That is, it now possible that 2 + Ri > 3 + Ri+1 for the highlighted alternates on the second row (2 and 3). (White boxes have much lower scores and will never be included, even with the addition of random noise.)
4mbn VLSEGEWQLVLHVWAKVE---ADVAGHGQDILIRLFKSHPETLEKFDRFKHLKTEAEMKASEDLKKHGVTVLTALGAILKKK
1r69 ----SISSRVKSKRIQLG---LNQAELAQKVGT----------------------------------TQQSIEQLENGK---
1r69 -------SISSRVKSKRIQLGLNQAELAQKVGT----------------------------------TQQSIEQLENGKTK-
1r69 ----SISSRVKSKRIQLG---LNQAELAQKVGT----------------------------------TQQSIEQLENGKTK-
1r69 -------SISSRVKSKRIQLGLNQAELAQKVGT----------------------------------TQQSIEQLENGKTKR
1r69 -------SISSRVKSKRIQLGLNQAELAQKVGT----------------------------------TQQSIEQLENGKTKR
1r69 -------SISSRVKSKRIQLGLNQAELAQKVGT----------------------------------TQQSIEQLENGKTK-
22244444444444444666666666666 666666666666542
Helix 1 Helix 2 Helix 3
4mbn GHHEAELKPLAQSHATKHKIPIKYLEFISEAIIHVLHSRHPGDFGADAQGAMNKALELFRKDIAAKYKELGYQG?
1r69 -------------------------TKRPRF-LPELASALG--VSVDWLLNG----------------------T
1r69 ---------------------------RPRF-LPELASALG--VSVDWLLNG----------------------T
1r69 ---------------------------RPRF-LPELASALG--VSVDWLLNG----------------------T
1r69 ----------------------------PRFlPELASALG---VSVDWLLNG----------------------T
1r69 ----------------------------PRF-LPELASALG--VSVDWLLNG----------------------T
1r69 ---------------------------RPRF-LPELASALG--VSVDWLLNG----------------------T
36661555555555 666666666
Helix 4 Helix 5
Figure 5: Sample Suboptimal Alignment. This shows what
happens if 434 repressor protein (1r69) is structurally aligned
to myoglobin (4mbn) six times with the addition of noise to the
alignment. Each of the six times gives a slightly different suboptimal
alignment for the less well conserved regions of the protein.
This allows one to readily distinguish between easy and hard to
align regions of the protein.
DHFR alignment
CORE ********* ********** ************ *************
MANU 1dhf LNCIVAVSQNMGIGKNGDLPWPPLRNEFRYFQRMTTTSSVEGKQ-NLVIMGKKTWFSI
MANU 8dfr LNSIVAVCQNMGIGKDGNLPWPPLRNEYKYFQRMTSTSHVEGKQ-NAVIMGKKTWFSI
MANU 4dfr ISLIAALAVDRVIGMENAMPWN-LPADLAWFKRNTL--------NKPVIMGRHTWESI
MANU 3dfr TAFLWAQDRDGLIGKDGHLPWH-LPDDLHYFRAQTV--------GKIMVVGRRTYESF
AUTO 1dhf LNCIVAVSQNMGIGKNGDLPWPPLRNEFRYFQRMTTTSSVEGKQ-NLVIMGKKTWFSI
AUTO 8dfr LNSIVAVCQNMGIGKDGNLPWPPLRNEYKYFQRMTSTSHVEGKQ-NAVIMGKKTWFSI
AUTO 4dfr ISLIAALAVDRVIGMENAMPW-NLPADLAWFKRNTLD--------KPVIMGRHTWESI
AUTO 3dfr TAFLWAQDRNGLIGKDGHLPW-HLPDDLHYFRAQTVG--------KIMVVGRRTYESF
MISMATCH |
CORE ********** **** ************** ***************
MANU 1dhf VPEKNRPLKGRINLVLSRELKEPPQGAHFLSRSLDDALKLTEQPELANKVDMVWIVGGSSVYKEAMNHP
MANU 8dfr VPEKNRPLKDRINIVLSRELKEAPKGAHYLSKSLDDALALLDSPELKSKVDMVWIVGGTAVYKAAMEKP
MANU 4dfr ---G-RPLPGRKNIILS-SQPGTDDRV-TWVKSVDEAIAACGDVP------EIMVIGGGRVYEQFLPKA
MANU 3dfr ---PKRPLPERTNVVLTHQEDYQAQGA-VVVHDVAAVFAYAKQHLDQ----ELVIAGGAQIFTAFKDDV
AUTO 1dhf -PEKNRPLKGRINLVLSRELKEPPQGAHFLSRSLDDALKLTEQPELANKVDMVWIVGGSSVYKEAMNHP
AUTO 8dfr -PEKNRPLKDRINIVLSRELKEAPKGAHYLSKSLDDALALLDSPELKSKVDMVWIVGGTAVYKAAMEKP
AUTO 4dfr -G---RPLPGRKNIILSSSQPGTDDRV-TWVKSVDEAIAACGDVPE-----.IMVIGGGRVYEQFLPKA
AUTO 3dfr -P--KRPLPERTNVVLTHQEDYQAQGA-VVVHDVAAVFAYAKQHLD----QELVIAGGAQIFTAFKDDV
CORE ********** * ** * ********
MANU 1dhf GHLKLFVTRIMQDFESDTFFPEIDLEKYKLLPEYPGVLSDVQEEKGIK------YKFEVYEKND---
MANU 8dfr INHRLFVTRILHEFESDTFFPEIDYKDFKLLTEYPGVPADIQEEDGIQ------YKFEVYQKSVLAQ
MANU 4dfr --QKLYLTHIDAEVEGDTHFPDYEPDDWE---SVFSEF---HDADAQNSHS---YCFEILERR----
MANU 3dfr --DTLLVTRLAGSFEGDTKMIPLNWDDFT---KVSSRT---VEDTNPALT----HTYEVWQKKA---
AUTO 1dhf GHLKLFVTRIMQDFESDTFFPEIDLEKYKLLPEYPGVLSDVQEEKG--I----KYKFEVYEK-N---
AUTO 8dfr INHRLFVTRILHEFESDTFFPEIDYKDFKLLTEYPGVPADIQEEDG--I----QYKFEVYQK-SV--
AUTO 4dfr --QKLYLTHIDAEVEGDTHFPDYEPDDWESVFSE------FHDADA--QNSHSSYCFEILER-R---
AUTO 3dfr --DTLLVTRLAGSFEGDTKMIPLNWDDFTKVSSR------TVEDTNPAL----THTYEVWQKKA---
Figure 6: Two Sample Multiple Alignments. This figure (adapted
from Gerstein & Levitt, submitted) shows sample multiple alignments
for two protein families. The first is for the dihydrofolate
reductase (DHFR) family, and the second, for the globin family.
For each family, in turn, two separate multiple alignments are
shown: the one marked "MANU" is a manually constructed
"gold-standard" from Gerstein et al. (1994), and the
one marked "AUTO" is automatically generated. The manually
and automatically generated alignments have been aligned as blocks
so that they have the fewest possible mismatches. Mismatches are
scored only in the core alignable regions, marked by a character
(e.g. "*") in the "CORE" row. They are flagged
in the automatically generated alignment (by double underlining,
changing case, and substituting "-" for ".").
The DHFR alignment has 1 mismatch in total and has 1dhf as the
central structure to which everything is aligned. The globin alignment
has 18 mismatches and has 1mbd as the central structure.
Globin alignment
CORE **************** ********************* *
MANU 2hhb-A ---------VLSPADKTNVKAAWGKVGA----HAGEYGAEALERMFLSFPTTKTYFPHF
MANU 2hhb-B --------VHLTPEEKSAVTALWGKV------NVDEVGGEALGRLLVVYPWTQRFFESF
MANU 2lhb PIVDTGSVAPLSAAEKTKIRSAWAPVYS----TYETSGVDILVKFFTSTPAAQEFFPKF
MANU 1mbd ---------VLSEGEWQLVLHVWAKVEA----DVAGHGQDILIRLFKSHPETLEKFDRF
MANU 2hbg ---------GLSAAQRQVIAATWKDIAG--ADNGAGVGKDCLIKFLSAHPQMAAVFG-F
MANU 1mba ---------SLSAAEADLAGKSWAPVFA----NKNANGLDFLVALFEKFPDSANFFADF
MANU 1ecd ----------LSADQISTVQASFDKVKG--------DPVGILYAVFKADPSIMAKFTQF
AUTO 2hhb-A ---------VLSPADKTNVKAAWGKVGA-H---AGEYGAEALERMFLSFPTTKTYFPHF
AUTO 2hhb-B ---------HLTPEEKSAVTALWGKV---N---VDEVGGEALGRLLVVYPWTQRFFESF
AUTO 2lhb ---------PLSAAEKTKIRSAWAPVYSTT---YETSGVDILVKFFTSTPAAQEFFPKF
AUTO 1mbd ---------VLSEGEWQLVLHVWAKVEA-D---VAGHGQDILIRLFKSHPETLEKFDRF
AUTO 2hbg ---------GLSAAQRQVIAATWKDIAG-A-DNGAGVGKDCLIKFLSAHPQMAAVFG-F
AUTO 1mba ---------SLSAAEADLAGKSWAPVFA-N---KNANGLDFLVALFEKFPDSANFFADF
AUTO 1ecd ----------LSADQISTVQASFDKVKG--------DPVGILYAVFKADPSIMAKFTQF
MISMATCH || | | ||||
CORE ********************* *****************
MANU 2hhb-A --DLS--------HGSAQVKGHGKKVADALTNAVAHV-------D--DMPNALSALSDLHAHKL-
MANU 2hhb-B -GDLSTP---DAVMGNPKVKAHGKKVLGAFSDGLAHL-------D--NLKGTFATLSELHCDKL-
MANU 2lhb KGLTTA----DQLKKSADVRWHAERIINAVNDAVASM-----DDT-EKMSMKLRDLSGKHAKSF-
MANU 1mbd -KHLKTE---AEMKASEDLKKHGVTVLTALGAILKK--------K-GHHEAELKPLAQSHATKH-
MANU 2hbg SGA-----------SDPGVAALGAKVLAQIGVAVSHL-----GDE-GKMVAQMKAVGVRHKGYGN
MANU 1mba KGKSVA-----DIKASPKLRDVSSRIFTRLNEFVNNA-----ANA-GKMSAMLSQFAKEHVGFG-
MANU 1ecd -AG-KDL---ESIKGTAPFETHANRIVGFFSKIIGEL------P---NIEADVNTFVASHKPRG-
AUTO 2hhb-A DLS----------HGSAQVKGHGKKVADALTNAVAHVD---D-----.MPNALSALSDLHAHKLR
AUTO 2hhb-B GDL----STPDAVMGNPKVKAHGKKVLGAFSDGLAHLD---N-----.LKGTFATLSELHCDKLH
AUTO 2lhb KGL----TTADELKKSADVRWHAERIINAVNDAVASMD---D---TEKMSMKLRDLSGKHAKSFQ
AUTO 1mbd KHL----KTEAEMKASEDLKKHGVTVLTALGAILKKkG---H-----.HEAELKPLAQSHATKHK
AUTO 2hbg SGA----SDPG-----..VAALGAKVLAQIGVAVSHLGDEGK-----.MVAQMKAVGVRH.kgyG
AUTO 1mba KGK----S-VADIKASPKLRDVSSRIFTRLNEFVNNAA---N---AGKMSAMLSQFAKEHVG.fG
AUTO 1ecd AGK-----DLESIKGTAPFETHANRIVGFFSKIIGELP---N-----.IEADVNTFVASHK.prG
MISMATCH |
CORE ******************** *******************
MANU 2hhb-A -RVDPVNFKLLSHCLLVTLAAHLP-A--EFTPAVHASLDKFLASVSTVLTSKYR------
MANU 2hhb-B -HVDPENFRLLGNVLVCVLAHHFG-K--EFTPPVQAAYQKVVAGVANALAHKYH------
MANU 2lhb -QVDPQYFKVLAAVIADTVAAG------------DAGFEKLMSMICILLRSAY-------
MANU 1mbd -KIPIKYLEFISEAIIHVLHSRHP-G--DFGADAQGAMNKALELFRKDIAAKYKELGYQG
MANU 2hbg KHIKAQYFEPLGASLLSAMEHRIGGKM---NAAAKDAWAAAYADISGALISGLQS-----
MANU 1mba --VGSAQFENVRSMFPGFVASVAAPP-----AGADAAWTKLFGLIIDALKAAGA------
MANU 1ecd --VTHDQLNNFRAGFVSYMKAHT------DFAGAEAAWGATLDTFFGMIFSKM-------
AUTO 2hhb-A ---VDPVNFKLLSHCLLVTLAAHLPAEFTPA VHASLDKFLASVSTVLTSKYR------
AUTO 2hhb-B ---VDPENFRLLGNVLVCVLAHHFGKEFTPP VQAAYQKVVAGVANALAHKY------H
AUTO 2lhb ---VDPQYFKVLAAVIADTVAAG-------- -DAGFEKLMSMICILLRSA.------Y
AUTO 1mbd ---IPIKYLEFISEAIIHVLHSRHPGDFGAD AQGAMNKALELFRKDIAAKYKELGYQG
AUTO 2hbg NKHIKAQYFEPLGASLLSAMEHRIGGKMNAA AKDAWAAAYADISGALISGLQS-----
AUTO 1mba ---VGSAQFENVRSMFPGFVASVAA--PPAG ADAAWTKLFGLIIDALKAAG------A
AUTO 1ecd ---VTHDQLNNFRAGFVSYMKAHTD---FAG AEAAWGATLDTFFGMIFSKM-------