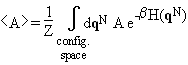 (6.1)
(6.1)Chapter 6 Methods for Computer Simulation
This chapter, the first on protein surfaces, will focus on developing methods of liquid simulation. These methods are embodied in a highly parallel liquid simulation program, which was used to generate the data for chapters 7, 8, and 9. This program was written from scratch and is discussed in appendix A.
I Monte-Carlo Methods
Of central importance in this work is the calculation of the average property
<A> of a liquid, such as the average dipole moment at a given point. Formally, this average is carried out in the canonical ensemble, i.e. at constant particle number N, volume V, and temperature T. In the N® ¥ limit, it involves summing the value of the property at every configuration qN in phase space, weighting each term by the Boltzmann factor.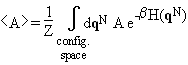 (6.1)
(6.1)
where H is the energy of the configuration
qN of liquid molecules, b = 1/kT, and Z (the
partition function) is 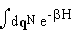 .
.
One approach to evaluating this integral and finding the average is to pick configurations in phase space randomly from a uniform distribution of all configurations, weight the property by the Boltzmann factor, and sum all the weighted terms. However, as the Boltzmann factor is small for most configurations - corresponding to molecular overlaps in the liquid - the sampling is inefficient. Metropolis et al. (1953) suggested a more efficient procedure. The configurations are picked at random according to the Boltzmann distribution and then summed without weighting.
Explaining how points are picked randomly according to the Boltzmann distribution is equivalent to explaining how given one configuration of a liquid, it is possible to generate another configuration such that resulting sequence of configurations is distributed according to the Boltzmann distribution. Mathematically, the distribution of liquid configurations can be represented by a vector r, such that a component rm of the vector represents the probability that the liquid has configuration m. If one has a given distribution of configurations rm, it is possible to generate a new distribution rn by a applying a transition matrix Tmn . A sequence of these configuration distributions, where one distribution depends only on the one immediately preceding it, is called a Markov chain. The essence of the Metropolis rule is constructing a transition matrix so that after applying it many times to an arbitrary starting distribution, one gets a Boltzmann distribution of configurations.
That is, at equilibrium, the liquid has to have the same Boltzmann distribution of states before and after application of the transition matrix, so
å r
m Tmn = rn = exp(-bHn)/Z (using Einstein summation convention). (6.2)The equilibrium condition does not uniquely determine the transition matrix, so it is customary to introduce a stronger requirement, called detailed balance, that the probability for a transition from configuration m to n be the same as that for n to m,
r
mTmn = rnTnm . (6.3)Detailed balance also does not uniquely determine the matrix, but Metropolis et al. were able propose one solution for T
mn that is consistent with it.|
rn = rm & n ¹ m |
T mn = amn |
|
|
r n < rm & n ¹ m |
T mn = (rn/rm) amn |
(6.4) |
|
n=m |
T mm = 1 - å rm Tmn (where n ¹ m ) |
|
where the matrix
amn is symmetric (amn = anm) and stochastic (anm are random probabilities such that the sum over n of anm is 1 ).The Metropolis solution for the transition matrix may appear a bit cryptic a first but is in practice just a simple rule for generating configurations. Start with a given configuration m of water molecules. There are a number of ways of replicating the effect of the symmetric, stochastic matrix
a. One of them is to rotate and translate a water molecule randomly according to a uniform probability distribution. This "move" generates a new configuration, denoted n. If the energy of the new configuration n is less than or equal to that of old configuration m, i.e. rn ³ rm, the first case of the Metropolis solution applies, and the move is accepted. If the energy of new configuration is greater than that of the old, the ratio of the probability of the two configurations, rn/rm = exp(-b(Hn - Hm)), is compared with a uniform random number between 0 and 1. If the ratio is greater than the random number, the "move" is accepted. Otherwise, configuration n is discarded, and one starts at configuration m again.Notice that as it is written in equation (6.4), the absolute probability
rn of a particular liquid configuration is virtually impossible to compute. For the correct normalization evaluating the integral in the partition function Z would be necessary. However, the Metropolis rule cleverly sidesteps this issue by requiring only the ratio rn/rm, in which the partition function cancels out.II Potential Functions for Liquids
A simple and standard form was used for the potential function between water molecules and between water and protein. Three terms were used for Coulomb electrostatics and Lennard-Jones attractions and repulsions.
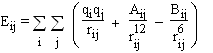 (6.5)
(6.5)
where A = 4es^12 and B = 4es^6 .
As summarized in table 6-1, the TIP3P model was used for the water parameters (Jorgensen et al., 1983). This is three-site model with partial charges on the hydrogens and oxygens and Lennard-Jones parameters only on the oxygen. The water was kept rigid throughout the simulation with fixed bond angles and distances.
The protein was also kept rigid and interacted with the water through the same Lennard-Jones and Coulomb terms as apply between waters. The CHARMM parameter set (Brooks et al., 1983) was used for the Lennard-Jones parameters and the partial charges on the protein. The TIP3P water potential was chosen because it is consistent with the CHARMM parameter set. The Lennard-Jones well depth and radius parameters for the water and the protein were combined using the Lorentz-Berthelot combination rules:
e
12 = sqrt(e1e2) (6.6)s
12 = (s1 + s2)/2Table 6-1
Potential Function Parameters|
atom |
e (kJ/mole) |
s (Å) |
charge (electrons) |
|
carbonyl carbon |
0.5023 |
3.7418 |
0.550 |
|
a -carbon (incorporating 1 hydrogen) |
0.2034 |
4.2140 |
0.100 |
|
b -carbon (incorporating 3 hydrogens) |
0.7581 |
3.8576 |
0.000 |
|
amide nitrogen |
0.9979 |
2.8509 |
-0.350 |
|
amide hydrogen |
0.2085 |
1.4254 |
0.250 |
|
carbonyl oxygen |
0.6660 |
2.8509 |
-0.550 |
|
water oxygen in interactions with the helix |
0.6660 |
2.8509 |
-0.834 |
|
water hydrogen in interactions with the helix |
0.2085 |
1.4254 |
0.417 |
|
water oxygen in interactions with other waters |
0.6367 |
3.1506 |
-0.834 |
|
water hydrogen in interactions with other waters |
0.0000 |
0.0000 |
0.417 |
The non-bonded parameters used in the simulation:
e and s are the two Lennard-Jones parameters and the charge is for standard Coulomb electrostatics. The water-water parameters are from the original TIP3P potential (Jorgensen et al., 1983), the water-helix interaction is taken directly from recent parameter sets in version 21.3 of CHARMM (Brooks et al., 1983) and version 2.1 of X-PLOR (Brünger et al., 1987). A number of other parameter sets were tried - in particular those for TIP4P water (Jorgensen et al., 1983) - but they were not found to affect the results significantly.