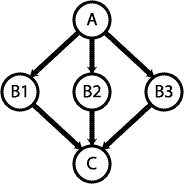
Combining three "othogonal" datasets can be modeled in a Bayesian network:

A pair of proteins is either interacting (positive) or not interacting (negative); this is represented by node A. Nodes B1, B2, and B3 represent the three "orthogonal" experiments with outcomes of either positive or negative. The outcome of node C is a prediction based on the information from the three experiments. The accuracy of this prediction can be expressed in terms of the conditional probability p(C|A), which is given by:
p(C|A) = p(C|B1,B2,B3) p(B1|A) p(B2|A) p(B3|A)
The conditional probabilities p(B1|A), p(B2|A) and p(B3|A) are functions of the accuracy of the individual experiments, thus, the overall prediction accuracy is also a function of these. The term p(C|B1,B2,B3) can be altered in order to change the outcome of the prediction. For instance, C can be chosen to be positive if any of the three experiment nodes have positive outcomes or if only one of them has a positive outcome, while the other two are negative (plus all other possible combinations). Obviously, this affects the overall accuracy of the prediction. However, in different situations, different trade-offs between sensitivity and specificity of the prediction might be desired.
The model equations have been put together in this Excel-spreadsheet.
The three experiments are "orthogonal" in the sense that there are no
direct connections between the nodes B1, B2 and B3.
They are conditionally independent, that is, if A is given, then
B1, B2 and B3 are independent.